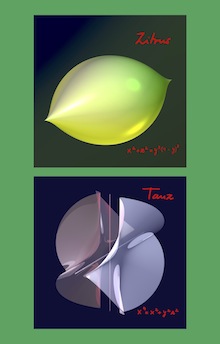
Acerca de la portada

(descargar)

Las portadas del volumen 20 de La Gaceta recogerán algunas imágenes de singularidades algebraicas, realizadas por Herwig Hauser (Universidad de Viena) y sus colaboradores usando SURFER (https://imaginary.org/program/surfer). Han formado parte de las distintas exposiciones Imaginary y se pueden encontrar ahora en la galería virtual «Herwig Hauser clásico» (https://imaginary.org/es/gallery/herwig-hauser-clasico). Los textos que las acompañan están escritos por el propio Hauser, a quien agradecemos su colaboración.

Zitrus (Limón): Esto no es un limón / La traición de las imágenes.

Al ver esta imagen, seguramente todos hemos pensado: «esto es un limón». Pero si es un limón, ¿por qué no tiene olor ni sabor? ¿Por qué no tiene ni poros ni manchas? ¡Está claro que esto no puede ser un limón!

[...] Las ecuaciones nos permiten construir modelos matemáticos que se parecen a las cosas, y estudiar estos modelos matemáticos nos ayuda, a su vez, a entender mejor la forma de las cosas. Como señaló Alfred H. S. Korzybski, «el mapa no es el territorio».

Todo esto forma parte de la «poesía» de las Matemáticas. A partir de ecuaciones algebraicas podemos generar bellas superficies que transportan nuestros pensamientos hasta rincones insospechados de nuestra mente.

Tanz (Danza): Recta que te quiero recta / Superficies regladas.

Las superficies regladas son las que se pueden generar mediante el movimiento de una recta que sigue un recorrido determinado. Aunque Danza no es reglada, contiene rectas [...]