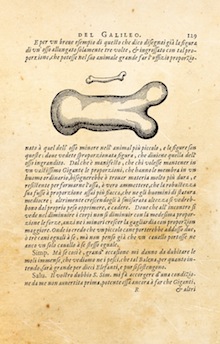
About the cover

(download)

Siguiendo con la conmemoración del Año de la Biología Matemática, traemos a este número de La Gaceta, además de un artículo en el que Marta Casanellas expone algunas aplicaciones del álgebra y la estadística a la biología, una portada que presenta una de las primeras obras científicas en las que se estudió la biología (en particular el crecimiento) con herramientas matemáticas: el Discorsi e dimostrazioni matematiche intorno a due nuove scienze, publicado en 1638 por Galileo Galilei. Ya en sus primeras páginas, que tratan de la resistencia de los sólidos, observa Galileo que si se construyen dos barcos, uno grande y uno pequeño, con las mismas proporciones y los mismos materiales, el mayor necesitará proporcionalmente más andamiaje y más soporte para poder botarlo sin que colapse por su propio peso. Y señala que lo mismo sucede con los animales, poniendo como ejemplo las distintas alturas desde las que pueden caer sin sufrir daño un caballo, un perro o un gato. [...]