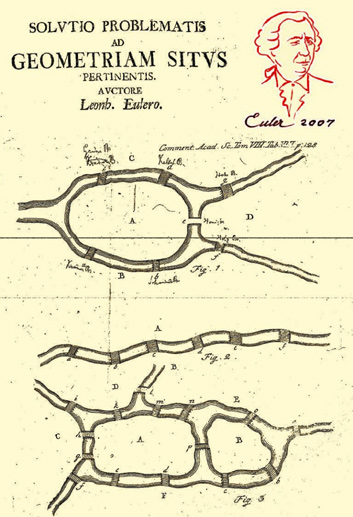
About the cover

Continuando con nuestro homenaje a Leonhard Euler al cumplirse 300 años de su nacimiento, en esta ocasión dedicamos la portada a uno de sus artículos más conocidos, Solutio problematis ad geometriam situs pertinentis (Solución de un problema relativo a la geometría de la posición). Euler presentó este trabajo ante la Academia de San Petersburgo el 26 de agosto de 1735, y apareció publicado en Commentarii academiae scientiarum Petropolitanae 8 (1741), pp. 128-140. El primer elemento de nuestra portada recoge el título del manuscrito y el nombre del autor tal y como aparecen en la publicación original.

El segundo elemento es la lámina con las figuras del artículo. Muchos de nuestros lectores reconocerán en la etiquetada como Fig. 1 el diagrama de los puentes de Königsberg, ciudad de Prusia Oriental cuyo nombre significa Montaña del Rey y a la que Euler se refiere, en latín, como Regiomons. [...]

Recordemos que el Problema de los Puentes de Königsberg consiste en decidir si es posible que un habitante de la ciudad pueda salir de paseo, atravesar exactamente una vez cada uno de los siete puentes que, como se ve en el diagrama (Fig. 1) unen los cuatro sectores en los que el río Pregel dividía Königsberg, y regresar a su casa. Euler observó que se trataba de un problema de geometría de la posición en el que las distancias no importaban, lo que hoy llamaríamos un problema topológico, y con frecuencia se considera este artículo de Euler como el nacimiento de la Topología.